金属管の曲げ加工計算 (S字)

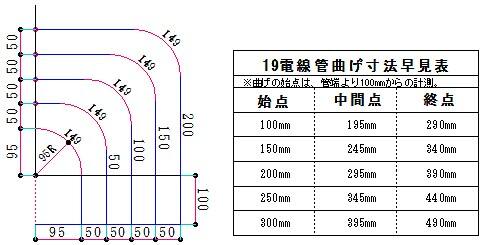
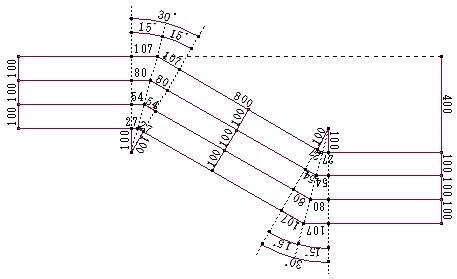
Ｓ字曲げの始点から終点までの計算方法
Ｓ字曲げ加工の始点から終点の求め方のご質問をいただきました。

 

Ｓ字曲げ加工の簡単な計算方法は、紹介しておきましたので、お分かりいただけているものだと思いますが、ご質問の30mmの上げ寸法では、最小寸法を下回るため、
私が紹介した簡単な計算方法では、寸法不足となってしまいます。

 

そこで、上げ寸法が小さく、ハイヒッキーで加工できない場合には、上げ角度を変更しなくてはならない場合もでてきます。

 

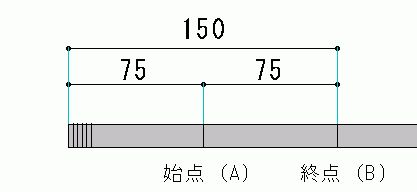
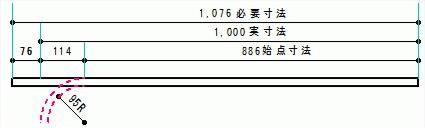
本編のＳ字曲げ加工で紹介しているように、電線管の端から、始点までの75mmという寸法は、19のハイヒッキーで加工する場合のほぼ最小寸法なので、この寸法より短い場合、Ｓ字加工を施すことが出来ません。

 

実際には、70mmが最小寸法ということになるので、ここでは70mmを基本とした計算方法を紹介しますので、参考にしてください。

始点と終点間を求める考え方

私のサイトでは、あくまで実践的な電気工事の方法を紹介しているので今回のような計算式を紹介することは、ほとんどありませんが、疑問をお持ちのみなさまの少しでもお役に立てればと、ご質問者様に解答する形で掲載させていただきます。

 

私が紹介した簡単な計算式だと角度30°の曲げ加工の場合、

高さ×２倍＝ なので、
30×2＝60mm　となりますから、最小寸法を下回ってしまいますので、曲げ加工を行うことが出来ません。

そこで、始点から終点までの寸法を 70mmとして、計算し直します。

 

考え方としては、『三平方の定理』を利用して計算します。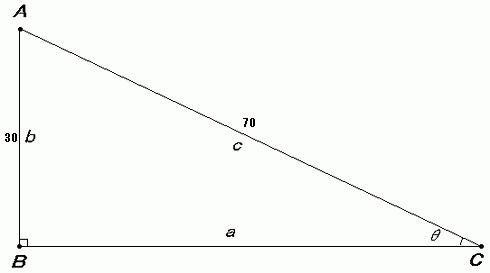

このように、直角三角形をイメージしてください。

まず、底辺を割り出します。

 

計算式は、ａ＝√c^2 - b^2となります。

 

この計算式から、
70^2 - 30^2＝4900 - 900＝4000　となり、
ａ（底辺）の長さは、√4000となります。

 

計算すると、63.2455320…ということですから、
ａ（底辺）の長さは、約63mmだと解ります。

 

これで、図のような直角三角形が描けます。

 

次に、曲げ角度を求めます。

 

計算式は、θ＝sin b/cなので、

 

30÷70＝sin 0.4285714…ということになります。

 

したがって、θ（角度）は、約25°となります。

 

ｃ（徐辺）を求める場合の計算式は、

 

ｃ＝√a^2＋b^2となります。

 

この計算式から、
63^2＋30^2＝√4869となり、
これを計算すると、69.778220…となり、
ｃ（徐辺）の寸法が、約70mmであることが求められます。

 

とまあ、こんな感じですが、実際に現場作業中にこんな計算をしている暇もないので、本文中で簡単な計算方法を紹介しています。

 

どうしても、計算したいと思うんだったら、関数電卓を利用すると簡単に計算することが出来ます。

 

・カシオ(CASIO) 関数電卓

 

ここで、パソコンのアクセサリーの中にある、電卓を使って関数計算を行う方法を紹介しておきましょう。

 

スタートメニュー⇒ 電卓を選択します。
すると下の画像のような電卓が出てきます。

 

この状態が普通の電卓と同じなので、関数電卓に切替えます。

左上の『』この部分をクリックします。
すると次のような機能選択ダイアログが出てくるので、赤いアンダーラインの『関数電卓』を選択します。
こうしておけば、Windows標準アクセサリーの電卓で簡単に計算することができるようにすることができます。

---

まとめ

 

各計算式は、下記を参照してください。

• ｃ（徐辺）ｃ＝√a^2＋b^2
• θ（角度）θ＝sin b/c
• ａ（底辺）ａ＝√c^2 - b^2

この『三平方の定理』は、構内柱の支線の長さを求めたりすることも出来ますし、図面を作成するときにも利用します。
というか、既に使ってると思いますけどね。

 

関数電卓も安くなりましたので、一つ持っておくと便利だと思います。

 

電気工事に使う工具をお探しなら下記サイトをご覧ください。